
And now with the with the height that we found, we confined the pressure. So now plug in for all the values, what we get is the height of 2.43 meters. We have the heights that chamber B is raised by and the cross sectional areas.

So we have the initial height column of chamber and B. But now we have big age in terms of values that we do know or we have previously found. This is pretty much just using algebra toe move things over, solve a big age. So once we saw this expression here for big age will get an equation that looks like this.

So now what we're gonna do once you finish writing this equation is we're going to solve for big age. We have be raised one meter high, so the water level is going to be, uh, lower in chamber beef if you were on the ground. Since remember, we have this, uh, height differentials. Excuse me will multiply that by the cross sectional area of chamber A for the term for chamber be. So we have big H that will be equal course.
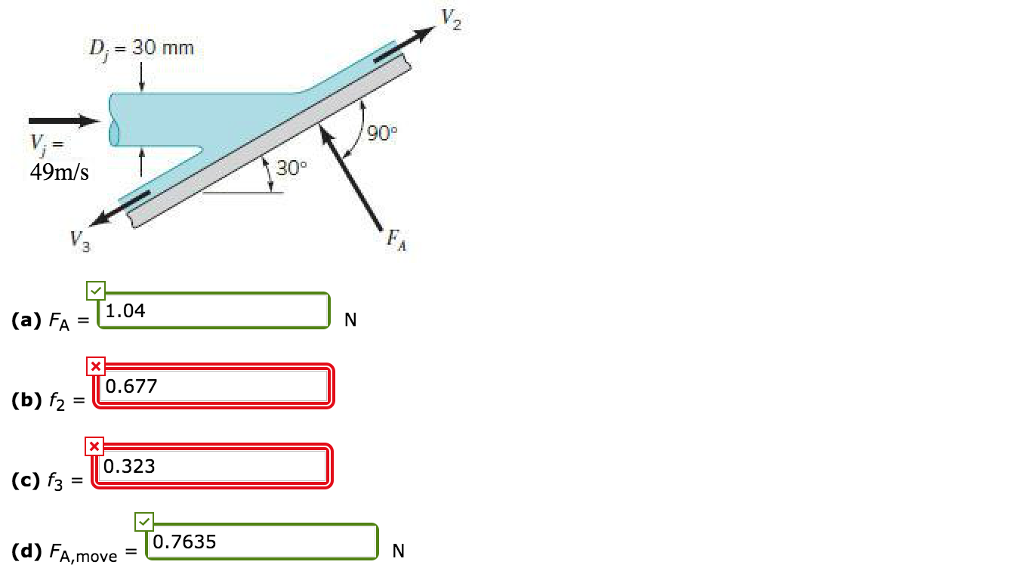
#DETERMINE THE MAGNITUE AND DIRECTION OF THE ANCHORING FORCE PLUS#
So what this is gonna look like? Yes, we'll have the cross sectional area a times the initial height, plus the cross sectional area B times the initial height in chamber B on and our new expression for the volume is going to look like this. So we can use this, uh, this expression for volume where we take the height, times, the the cross sectional area, and we can set that equal to a new expression for the volume in terms of the new height that we're looking for. So we know that the volume of water hasn't changed. So we're now looking for this new height age, Andi in chamber B, it'll be h minus little h. So as you can see, here we have when the water lines or level. Once we open, it's That means that the system will be in on equilibrium and the height, the level of water will be equal. We'll get a pressure of 130.8 killer Pascal's On the second part of this problem, we want to find what the pressure of the valve would be. So the term that we would use here for the height would be H B plus h so two plus one that would just be three Onda. But just for the term H where we do the height, it's not just going to be two meters that since this chamber is lifted, uh, a level h off the ground, which we know is one meter. Now for chamber B, it's gonna be pretty similar. So when we do that, we're going to get a pressure of 111 0.1 killer pass cables. So first solve for the pressure due to chamber a zoo on this side and we'll do is we'll take the atmospheric pressure and we'll add an expression for Delta P, where we take the density of water, time to gravitational acceleration times the height of a, which we just found. So now that we have the height of the water, we can go ahead and sold for the pressure on either side of these two red points. And in chamber B, we'll find that it's two meters. We'll find that we have a height of one meter, so that's the height of the column of water. So when we put in for the values that we have for, uh, chamber A So the massive water on the cross sectional area of chamber A. We have the mass divided by density on the cross sectional area. We get an expression that looks like this. The second where we take the height, which is what we're looking for, multiply it by the cross sectional area.
The first where we take the mass and divided by the density. So we can do this by rating two expressions for the volume.

So first gonna do is we're gonna write an expression to, uh, find what the height of each water column in the chambers is. We want to find the pressure on either side of the valve. We have this system here where we have a valve, it's closed.


 0 kommentar(er)
0 kommentar(er)
